# Binius STARKs分析及其優化## 1. 引言STARKs效率低下的一個主要原因是實際程序中大多數數值都較小,但爲了確保基於Merkle樹證明的安全性,使用Reed-Solomon編碼對數據進行擴展時,許多額外的冗餘值會佔據整個域。降低域的大小成爲了關鍵策略。第1代STARKs編碼位寬爲252bit,第2代爲64bit,第3代爲32bit,但32bit編碼位寬仍存在大量浪費空間。二進制域允許直接對位進行操作,編碼緊湊高效而無任意浪費空間,可能是第4代STARKs。Binius使用基於塔式二進制域的算術化、改進版的HyperPlonk乘積與置換檢查、小域多項式承諾等技術,從各個角度提升效率。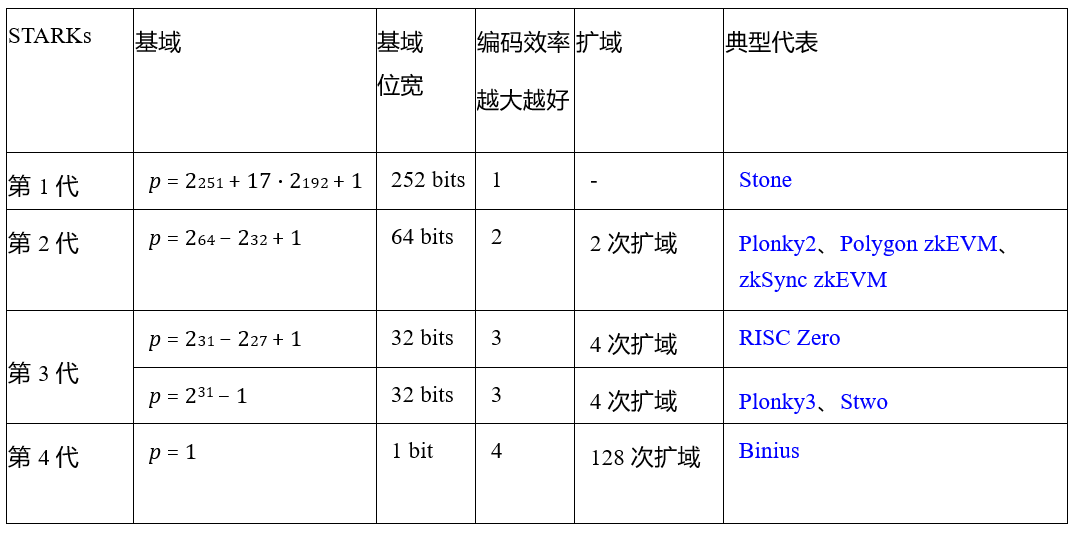## 2. 原理解析Binius由五項關鍵技術組成:1. 基於塔式二進制域的算術化2. 改編版HyperPlonk乘積與置換檢查 3. 新的多線性移位論證4. 改進版Lasso查找論證5. 小域多項式承諾方案### 2.1 基於塔式二進制域的算術化塔式二進制域支持高效的算術操作和簡化的算術化過程。二進制域元素可以直接映射到k位的字符串,具有一對一映射的便利性。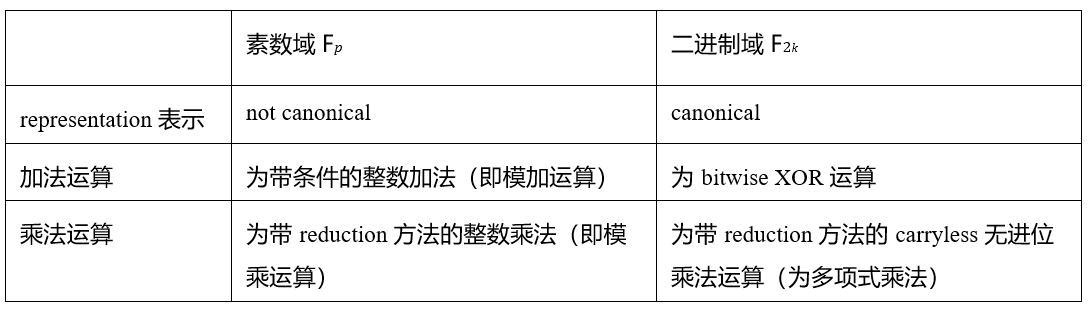### 2.2 改編版HyperPlonk乘積和置換檢查Binius借鑑了HyperPlonk的核心檢查機制,包括GateCheck、PermutationCheck、LookupCheck等,並在以下方面做出改進:- ProductCheck優化- 除零問題的處理- 跨列PermutationCheck### 2.3 新的多線性移位論證Binius引入了Packing和移位運算符兩個關鍵方法來構造和處理虛擬多項式。### 2.4 改編版Lasso查找論證Binius將Lasso適應於二進制域的操作,引入了乘法版本的Lasso協議。### 2.5 小域多項式承諾Binius提供了兩種基於二進制域的Brakedown多項式承諾方案,主要使用小域多項式承諾與擴展域評估、小域通用構造和塊級編碼與Reed-Solomon碼技術。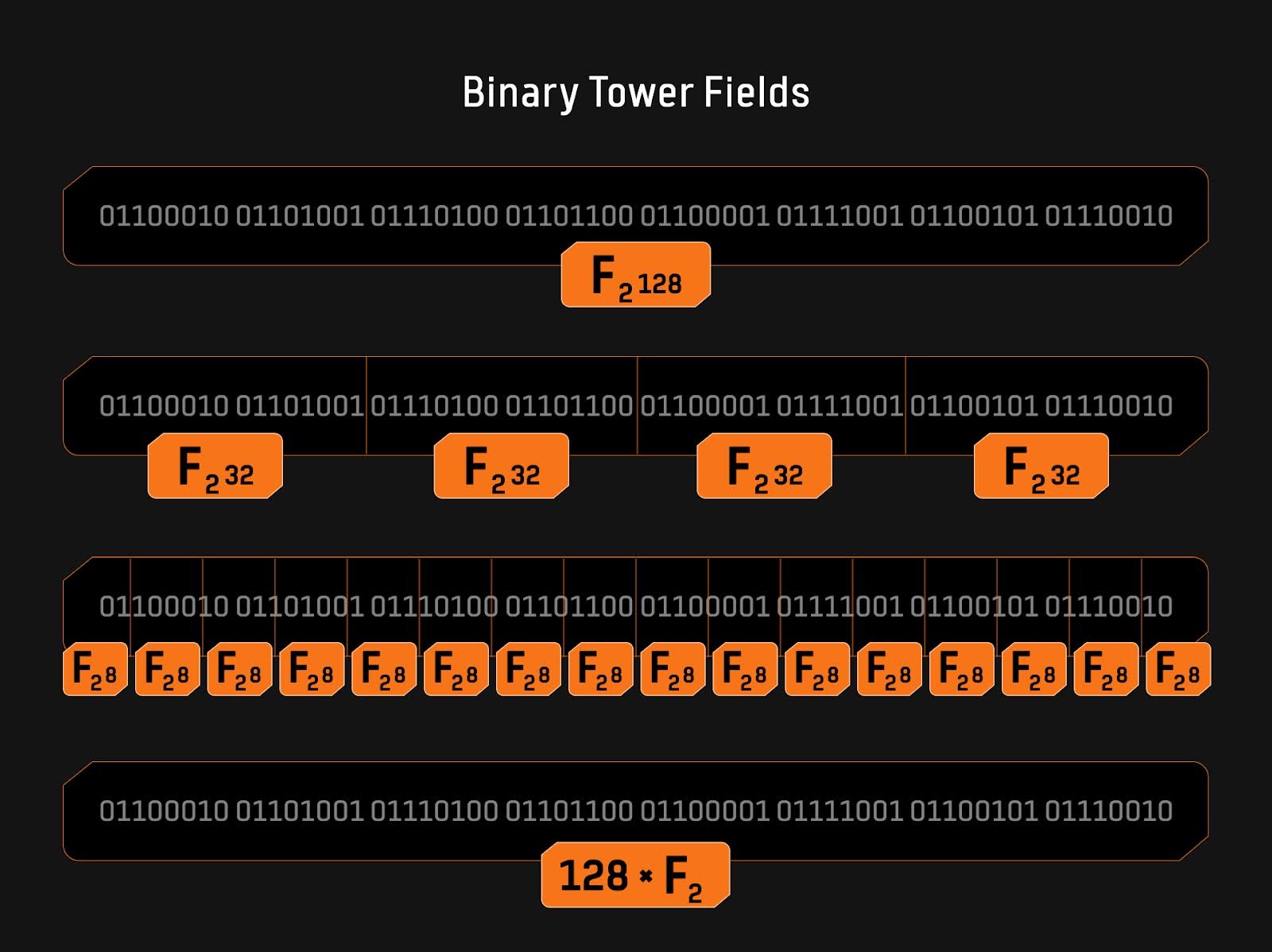## 3. 優化思考### 3.1 GKR-based PIOP基於GKR的二進制域乘法運算算法,通過將"檢查2個32-bit整數A和B是否滿足A·B =? C",轉換爲"檢查中(gA)B =? gC 是否成立",借助GKR協議大幅減少承諾開銷。### 3.2 ZeroCheck PIOP優化通過在證明方和驗證方之間調整工作量分配,提出了多種優化方案:- 減少證明方的數據傳輸- 減少證明方評估點的數量 - 代數插值優化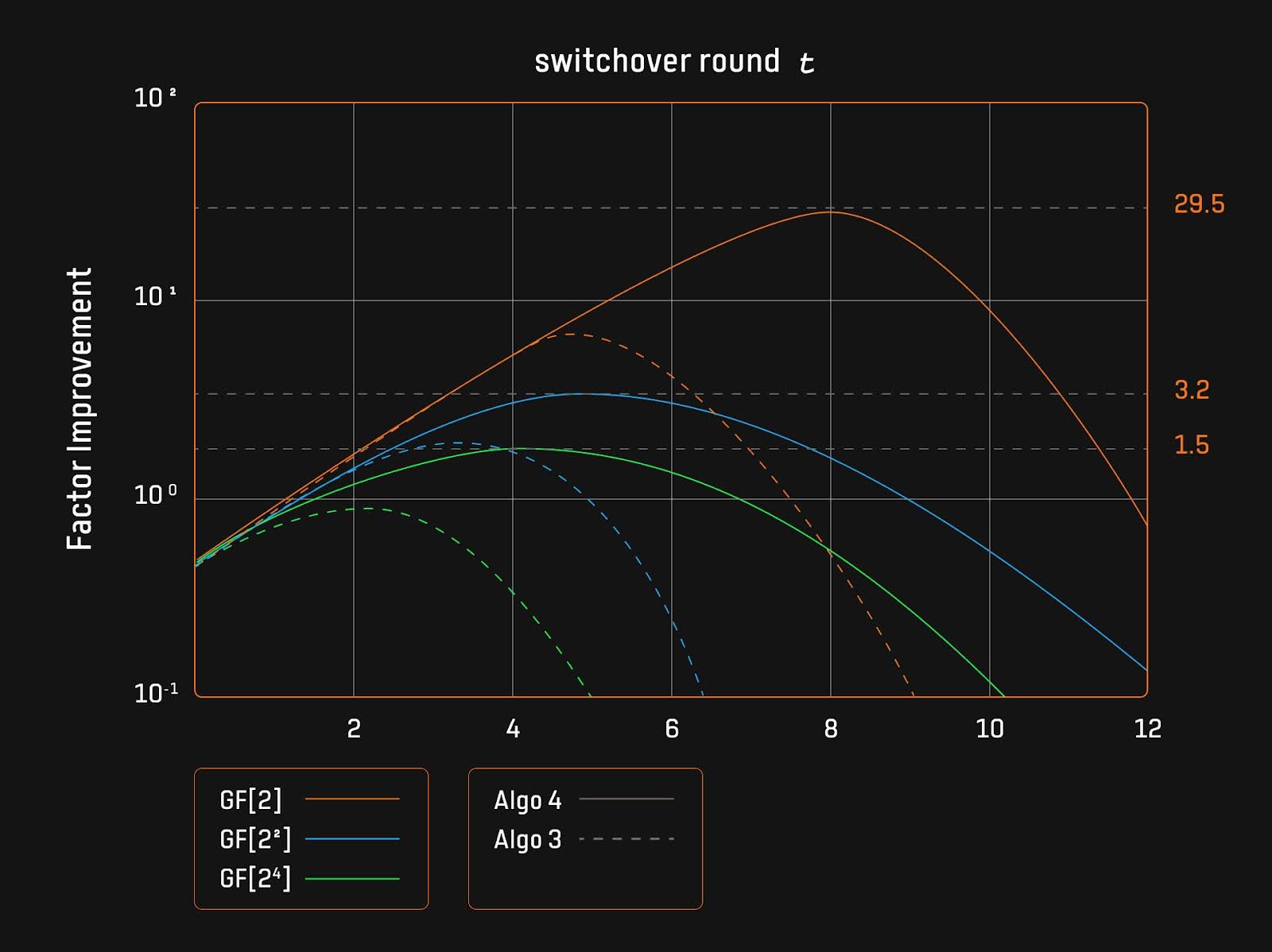### 3.3 Sumcheck PIOP優化Ingonyama提出了針對基於小域的Sumcheck協議的改進方案,集中於切換輪次t的選擇。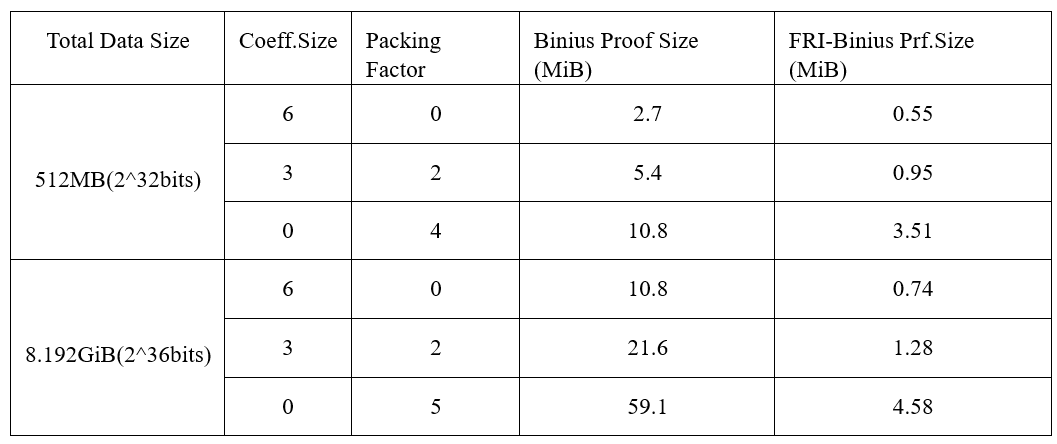### 3.4 PCS優化:FRI-Binius FRI-Binius實現了二進制域FRI折疊機制,帶來4個方面的創新:- 扁平化多項式- 子空間消失多項式- 代數基打包 - 環交換SumCheck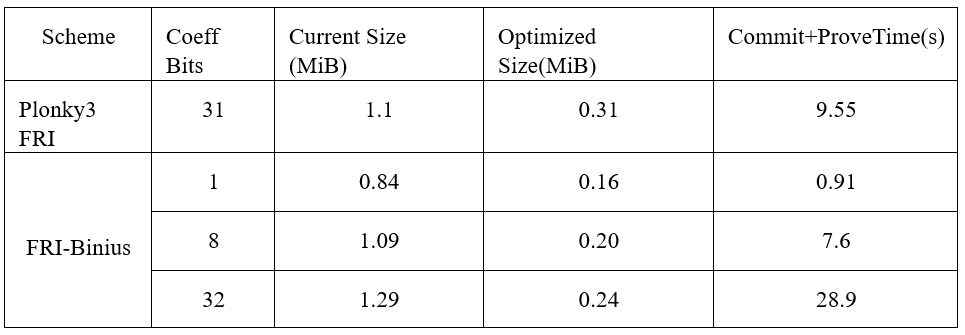## 4. 小結Binius是"使用硬件、軟件、與FPGA中加速的Sumcheck協議"的協同設計方案,可以以非常低的內存使用率來快速證明。Binius中已基本完全移除了Prover的commit承諾瓶頸,新的瓶頸在於Sumcheck協議,而這可借助專用硬件高效解決。FRI-Binius方案爲FRI變體,可從域證明層中消除嵌入開銷,而不會導致聚合證明層的成本激增。當前,多個團隊正在開發Binius相關技術,包括遞歸層、zkVM等。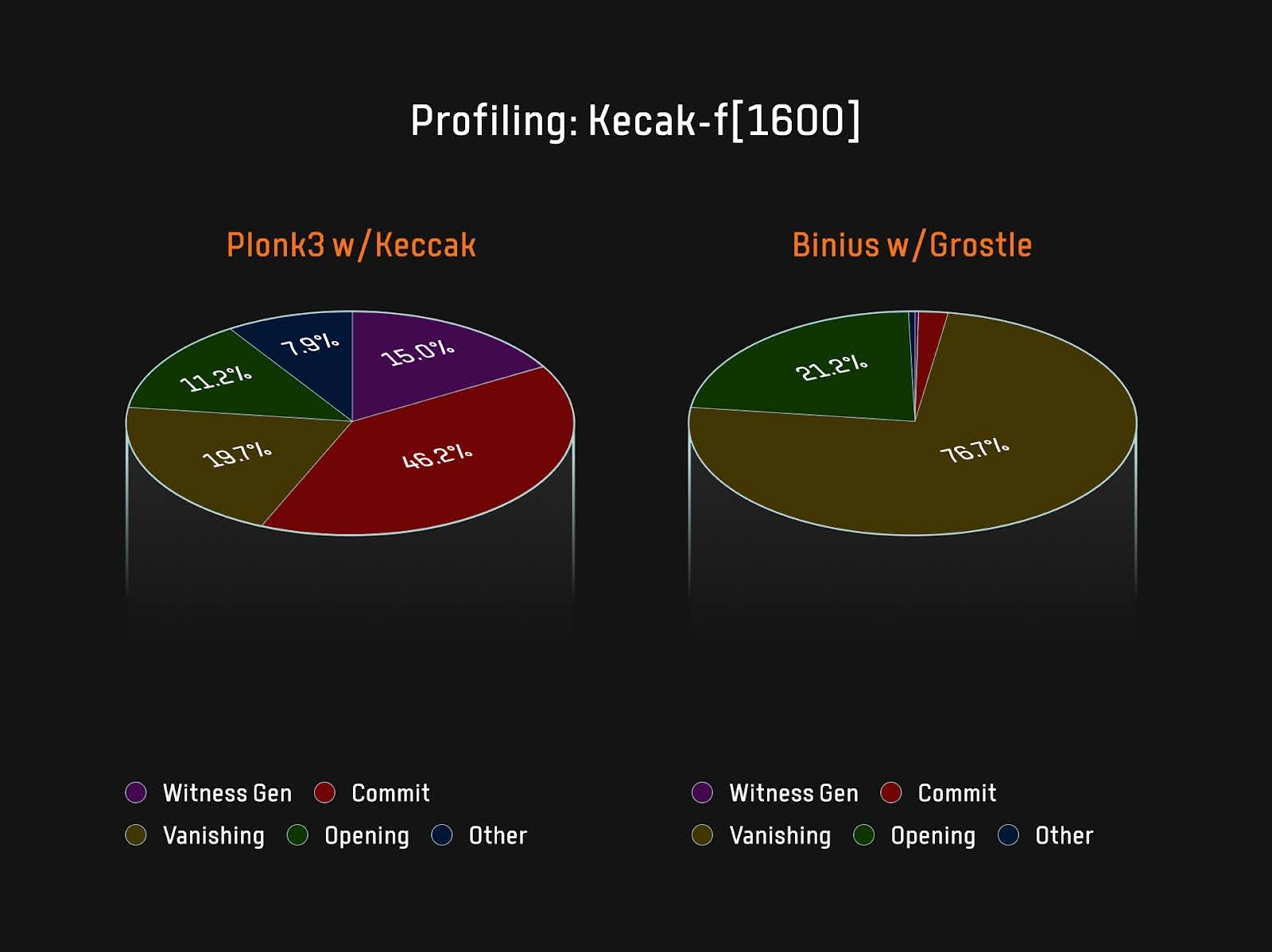
Binius創新突破:基於二進制域的高效STARK方案解析
Binius STARKs分析及其優化
1. 引言
STARKs效率低下的一個主要原因是實際程序中大多數數值都較小,但爲了確保基於Merkle樹證明的安全性,使用Reed-Solomon編碼對數據進行擴展時,許多額外的冗餘值會佔據整個域。降低域的大小成爲了關鍵策略。
第1代STARKs編碼位寬爲252bit,第2代爲64bit,第3代爲32bit,但32bit編碼位寬仍存在大量浪費空間。二進制域允許直接對位進行操作,編碼緊湊高效而無任意浪費空間,可能是第4代STARKs。
Binius使用基於塔式二進制域的算術化、改進版的HyperPlonk乘積與置換檢查、小域多項式承諾等技術,從各個角度提升效率。
2. 原理解析
Binius由五項關鍵技術組成:
2.1 基於塔式二進制域的算術化
塔式二進制域支持高效的算術操作和簡化的算術化過程。二進制域元素可以直接映射到k位的字符串,具有一對一映射的便利性。
2.2 改編版HyperPlonk乘積和置換檢查
Binius借鑑了HyperPlonk的核心檢查機制,包括GateCheck、PermutationCheck、LookupCheck等,並在以下方面做出改進:
2.3 新的多線性移位論證
Binius引入了Packing和移位運算符兩個關鍵方法來構造和處理虛擬多項式。
2.4 改編版Lasso查找論證
Binius將Lasso適應於二進制域的操作,引入了乘法版本的Lasso協議。
2.5 小域多項式承諾
Binius提供了兩種基於二進制域的Brakedown多項式承諾方案,主要使用小域多項式承諾與擴展域評估、小域通用構造和塊級編碼與Reed-Solomon碼技術。
3. 優化思考
3.1 GKR-based PIOP
基於GKR的二進制域乘法運算算法,通過將"檢查2個32-bit整數A和B是否滿足A·B =? C",轉換爲"檢查中(gA)B =? gC 是否成立",借助GKR協議大幅減少承諾開銷。
3.2 ZeroCheck PIOP優化
通過在證明方和驗證方之間調整工作量分配,提出了多種優化方案:
3.3 Sumcheck PIOP優化
Ingonyama提出了針對基於小域的Sumcheck協議的改進方案,集中於切換輪次t的選擇。
3.4 PCS優化:FRI-Binius
FRI-Binius實現了二進制域FRI折疊機制,帶來4個方面的創新:
4. 小結
Binius是"使用硬件、軟件、與FPGA中加速的Sumcheck協議"的協同設計方案,可以以非常低的內存使用率來快速證明。Binius中已基本完全移除了Prover的commit承諾瓶頸,新的瓶頸在於Sumcheck協議,而這可借助專用硬件高效解決。
FRI-Binius方案爲FRI變體,可從域證明層中消除嵌入開銷,而不會導致聚合證明層的成本激增。當前,多個團隊正在開發Binius相關技術,包括遞歸層、zkVM等。
现在开始继续用中文完成评论,记住要符合人设和语言要求:写出一条评论。
老司机又探路,这技术香啊